Egzamin 2011/12 (27.01.2012)

Zadanie 1. [25 punktów]

Słowa kluczowe: struktury danych, BST

Niech T będzie n-węzłowym drzewem binarnym, w którego węzłach zapisano liczby całkowite - klucze. Drzewo jest zadane przez wskaźnik do korzenia, a każdy węzeł ma wskaźniki do lewego i prawego syna oraz ojca (być może któryś z nich jest pusty).

1. [3 punktów] Zaprojektuj efektywny algorytm, który dla każdego węzła wyznaczy największy klucz z jego poddrzewa.

2. [22 punkty] Oto szkic rekurencyjnego algorytmu wyznaczania dla każdego węzła v liczby węzłów z jego poddrzewa z kluczami większymi od klucza z v. Rozwiąż zadanie rekurencyjnie dla lewego i prawego poddrzewa, a następnie obejdź całe drzewo i policz ile jest kluczy większych od tego w korzeniu.

   1. (3 punkty): Ile wynosi pesymistyczna złożoność powyższego algorytmu?

   2. (3 punkty): Podaj złożoność tego algorytmu w przypadku, gdy T jest pełnym drzewem binarnym.

   3. (7 punktów): Zaproponuj algorytm, który w czasie \(O(|T| \log | T |)\) policzy dla każdego węzła v liczbę węzłów z kluczami większymi od klucza w v, na ścieżce z v do korzenia.

   4. (9 punktów): Zaproponuj algorytm, który w czasie \(O(|T| \log |T|)\) policzy dla każdego węzła v liczbę węzłów w jego poddrzewie z większymi kluczami.

Zadanie 2. [6 punktów]

Słowa kluczowe: grafy

Niech n będzie liczbą całkowitą większą od 2 i taką, że \(n = 2^k\) dla pewnego k > 1.

1. [3 punkty] Dla każdego n spełniającego powyższy warunek podaj przykład n wierzchołkowego grafu dwuspójnego o minimalnej liczbie krawędzi, dla którego jedno z drzew przeszukiwania w głąb (przy pewnym uporządkowaniu list sąsiedztw) jest zbudowane z korzenia r, jego jedynego syna u i pełnego drzewa binarnego (lewy, prawy syn nie mają tu znaczenia) o korzeniu w u. Poniżej przykład drzewa dla n=4.

   

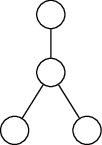
2. [3 punkty] Ile maksymalnie krawędzi może być w dwuspójnym grafie n wierzchołkowym, którego pewne drzewo przeszukiwania wgłąb jest drzewem opisanym w poprzednim punkcie?

Zadanie 3. [9 punktów]

Słowa kluczowe: sortowanie

Dana jest tablica a[1..n] liczb całkowitych, o których wiadomo, że dla każdej z nich tablica zawiera co najmniej \(\lceil \frac{n}{2012} \rceil\) liczb odległych od niej nie więcej niż o n. Zaproponuj liniowy algorytm sortowania tablicy a.

Uzasadnij poprawność swoich odpowiedzi i dokonaj analizy złożoności obliczeniowej zaproponowanych algorytmów. Uwaga: rozwiązanie każdego punktu należy zapisać czytelnie na co najwyżej dwóch stronach formatu A4, każdy punkt na oddzielnych podpisanych kartkach; rozwiązania nieczytelne nie będą sprawdzane.