Egzamin poprawkowy 2021/22 (21.02.2022)#

Zadanie 1 [7 punktów]#

Słowa kluczowe: struktury danych, Find-Union, drzewa

W tablicy \(P[1,\ldots,n]\) opisano n-wierzchołkowe drzewo z korzeniem. Wierzchołki drzewa ponumerowano liczbami \(1, 2, \ldots, n\) i każdy wierzchołek jest identyfikowany z jego numerem. Jeżeli wierzchołek v nie jest korzeniem , to \(P[v]\) jest rodzicem wierzchołka v w drzewie. Wierzchołek v jest korzeniem wtedy i tylko wtedy, gdy \(P[v] = v\). Na początku wszystkie wierzchołki są czarne.

Na drzewie wykonujemy następujące operacje:

  • Przekoloruj(v,k):: każdy z czarnych wierzchołków spośród \(v, P[v], P[P[v]], \ldots, P^{k}[v]\) zamień na biały \((k \ge 0, P^{0}[v] = v)\),

  • DłBiałej(v):: podaj długość najdłuższej białej ścieżki o początku w wierzchołku v w kierunku do korzenia (wierzchołki na ścieżce nie mogą się powtarzać).

Zaproponuj strukturę danych, która umożliwi wydajne wykonanie ciągu \(m > n\) operacji Przekoloruj i DłBiałej przy założeniu, że kolejność wykonywania tych operacji może być dowolna.

Podpowiedź

Użyj struktury Find-Union. Ciąg m operacji Przekoloruj i DłBiałej można wykonać w czasie \(O(m\alpha(n))\).

  • Zbiory powinny reprezentować spójne poddrzewa o czarnym korzeniu i pozostałych białych wierzchołkach. Jedyny wyjątek może dotyczyć zbioru który zawiera korzeń całego drzewa, taki zbiór może składać się z samych białych wierzchołków.

  • Każdy zbiór powinien zawierać wskaźnik do czarnego wierzchołka (wystarczy prosta modyfikacja Union)

  • Każdy wierzchołek pamięta swoją głębokość w drzewie (obliczoną podczas preprocessingu drzewa)

Przykładowe drzewo z częściowo przekolorowanymi wierzchołkami:

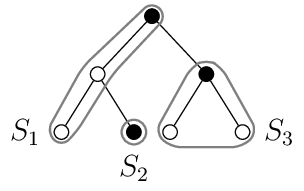
Figure made with TikZ

Zadanie 2 [10 punktów]#

Słowa kluczowe: grafy

Powiemy, że graf nieskierowany G jest prawie drzewem wtedy i tylko wtedy, gdy jest spójny i każda jego krawędź należy do co najwyżej jednego cyklu elementarnego.

  1. [6 punktów] Załóżmy, że G jest grafem ważonym o dodatnich wagach na krawędziach. Zaproponuj wydajny algorytm, który dla danego źródła s policzy wagi najlżejszych ścieżek prowadzących z s do wszystkich pozostałych wierzchołków.

  2. [4 punkty] Powiemy, że prawie drzewo jest maksymalne gdy, każda krawędź należy do jakiegoś cyklu elementarnego.

    1. Ile wynosi minimalna a ile maksymalna wysokość BFS drzewa w maksymalnym n-wierzchołkowym prawie drzewie?

    2. Ile wynosi minimalna a ile maksymalna wysokość DFS drzewa w maksymalnym n-wierzchołkowym prawie drzewie? Uwaga: cyklem elementarnym nazywamy cykl o długości co najmniej 3, którego wierzchołki są parami różne. Ponadto możesz przyjąć, że \(n \ge 3\).

Zadanie 3 [9 punktów]#

Słowa kluczowe: sortowanie

Dokonaj analizy następującego, rekurencyjnego algorytmu sortowania tablicy \(a[1..n]\), dla \(n > 0\).

Sort(i,j){
    // 1 <= i <= j <= n
    if (i + 1) = j then if a[i] > a[j] then a[i] :=: a[j]; // zamiana wartości zmiennych
    if (i+1) < j then {
        s := ceil(2(j - i + 1)/3);
        Sort(i,i+s-1); Sort(j-s+1,j); Sort(i,i+s-1)
    }
}

  1. [2 punkty] Udowodnij, że wywołanie Sort(1,n) posortuje tablicę a niemalejąco.

  2. [3 punkty] Ile razy zamiana \(a[i] :=: a[j]\) zostanie dokonana dla \(n = 4k\) i \(a[1,\ldots,n] = [n, 1, n-2, 3, \ldots, 2, n-1]\)?

  3. [4 punkty] Dokonaj analizy pesymistycznej złożoności Sort(1,n) ze względu na liczbę porównań pomiędzy elementami tablicy a.

Zadanie 4 [14 punktów]#

Słowa kluczowe: teksty

W tym zadaniu rozważamy niepuste słowa nad alfabetem \(\{a,b\}\) o długości \(n > 2\), w których pierwszym symbolem jest zawsze a.

  1. [2 punkty] Dla ilu słów o początku ab każda z wartości w tablicy prefiksów-sufiksów jest nie większa od 1?

  2. [4 punkty] Dla ilu słów o początku aa każda z wartości w tablicy prefiksów-sufiksów jest nie większa od 1?

  3. [8 punktów] Zaproponuj wydajny algorytm, który dla danego słowa x o długości n obliczy tablicę \(W[1,\ldots,n]\) taką, że \(W[i]\) jest liczbą wszystkich różnych podsłów w sufiksie \(x[i,\ldots,n]\).

Uzasadnij poprawność swoich rozwiązań i dokonaj analizy złożoności obliczeniowej zaproponowanych algorytmów.

Podpowiedź

Podzadanie c:

Tablicę W można obliczyć w czasie \(O(n)\) za pomocą drzewa sufiksowego. Wartość \(W[1]\) oznacza liczbę różnych podsłów w całym słowie, którą możemy obliczyć za pomocą algorytmu z ćwiczeń. Pozostałe wartości obliczamy wg wzoru \(W[i]=W[i-1]-C(i)\), gdzie \(C(i)\) oznacza liczbę prefiksów podsłów \(x[i,\ldots,n]\), które nie występują w \(x[i+1,\ldots,n]\).

Wartości \(C(i)\) możemy wyznaczyć w czasie \(O(1)\) jeśli wzbogacimy drzewo sufiksowe o następujące atrybuty:

  • \(h(v)\): sumę długości krawędzi na ścieżce do korzenia

  • \(lastOcc(v)\): indeks najpóźniejszego sufiksu w poddrzewie (który rozpoczyna się najbardziej na prawo)

  • \(up(v)\): najwyższy przodek o tej samej wartości \(lastOcc\) (zauważmy, że wartości \(lastOcc\) tworzą spójne ścieżki)