Egzamin 2024/25 (4.02.2025)#
Zadanie 1 [15 punktów]#
Niech n będzie dodatnią liczbą całkowitą i niech \(A = \langle a_1, a_2, \ldots , a_n\rangle\) będzie ciągiem parami różnych liczb całkowitych. Przez h(A) oznaczamy wysokość drzewa wyszukiwań binarnych powstałego w wyniku wstawienia do początkowo pustego drzewa kolejno liczb \(a_1, a_2, \ldots, a_n\). Wysokość mierzymy liczbą krawędzi.
[5 punktów] Zaprojektuj algorytm, asymptotycznie optymalny ze względu na porównania, sortujący ciągi A, o których wiadomo, że h(A) jest nie mniejsze od n - 2025.
[4 punkty] Zaprojektuj algorytm, asymptotycznie optymalny ze względu na porównania, sortujący ciągi A, o których wiadomo, że h(A) jest nie mniejsze od n/2025.
[6 punktów] Przyjmij, że elementami ciągu A są liczby \(1, 2, \ldots, n\) i h(A) = n-1. Ciąg A zapisano w tablicy a[1..n]. Zaprojektuj wydajny algorytm sprawdzający, na której pozycji w ciągu A jest liczba x, dla pewnego \(x \in \{1, 2, \ldots, n\}\).
Zadanie 2 [10 punktów]#
Dane jest drzewo binarne T, w którego węzłach zapisano parami różne klucze całkowitoliczbowe. Każdy węzeł ma atrybuty: R (rodzic), L (lewe dziecko), P (prawe dziecko), K (klucz). Dostęp do drzewa jest przez jego korzeń.
[4 punkty] Zaproponuj wydajny algorytm, który sprawdzi, czy wykonując tylko zamiany dzieci węzłów lewy/prawy można otrzymać drzewo wyszukiwań binarnych.
[6 punktów] Zaprojektuj strukturę danych, która pozwoli wykonywać na drzewie T wydajnie następujące operacje:
Init(T):: zainicjuj strukturę danych (operacja wykonywana tylko raz na początku)
Swap(x):: jeśli x jest kluczem w drzewie T, to zamień dzieci węzła zawierającego x
isBst(x):: jeśli x jest kluczem w drzewie T, to sprawdź czy poddrzewo o korzeniu zawierającym x jest drzewem wyszukiwań binarnych
Podaj czasy tworzenia struktury i wykonywania poszczególnych operacji.
Zadanie 3 [5 punktów]#
Dane są trzy słowa \(x_1\), \(x_2\) i y nad skończonym alfabetem \(\Sigma\), \(|x_1|, |x_2| \le |y|\). Powiemy, że podsłowo \(y[i..j]\) poprzedza podsłowo \(y[k..l]\) wtedy i tylko wtedy, \(j < k\). Zaprojektuj wydajny algorytm, który policzy ile jest par indeksów (i, k) takich, że \(y[i..i+|x_1|-1] = x_1\), \(y[k..k+|x_2|-1] = x_2\) i \(y[i..i+|x_1|-1]\) poprzedza \(y[k..k+|x_2|-1]\).
Zadanie 4 [10 punktów]#
Dla dodatniej liczby całkowitej n, grafem trapezowym rzędu n nazywamy każdy graf :math:({1,2, ldots , 2n}, E}`, w którym \(E = E_1 \cup E_2\), gdzie \(E_1 = \{1-2, (2n-1)-2n,\quad 1-3, 3-5, \ldots, (2n-3)-(2n-1),\quad 2-4, 4-6, \ldots, (2n-2)-2n\}\), natomiast
\(E_2\) jest zbiorem krawędzi \(u-v\), gdzie u jest nieparzyste i \(1 < u < 2n-1\), natomiast v jest parzyste i \(2 < v < 2n\) oraz dla każdej pary różnych krawędzi \(u_1-v_1\), \(u_2-v_2\), \(u_1 < u_2\) i \(v_1 < v_2\) lub \(u_2 < u_1\) i \(v_2 < v_1\). Krawędzie ze zbioru \(E_1\) nazywamy krawędziami zewnętrznymi, natomiast krawędzie ze zbioru \(E_2\) nazywamy - wewnętrznymi.
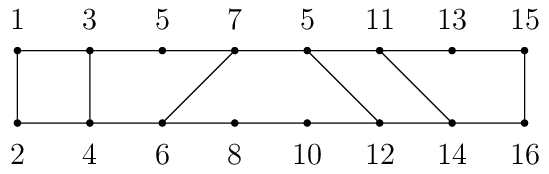
Przykład grafu trapezowego
[3 punkty] Dana jest liczba n i zbiór krawędzi \(E_2\). Zaprojektuj wydajny algorytm, który sprawdzi, czy graf G = \((\{1, 2, \ldots , 2n\}, E_1 \cup E_2)\) jest grafem trapezowym.
[2 punkty] Dla grafu z przykładu podaj największą i najmniejszą wysokość możliwego DFS- drzewa o korzeniu w wierzchołku 1.
[5 punktów] Zaprojektuj strukturę danych umożlwiającym na dynamicznym grafie G rzędu n wydajne wykonywanie następujących m > n operacji:
\(Ini(E_2)\):: zainicjuj strukturę danych dla \(G = ({1, 2, \ldots , 2n}, E_1 \cup E_2)\); operacja wykonywana tylko raz na samym początku
Usuń(u,v):: jeśli \(u-v\) jest krawędzią wewnętrzną w G, to usuń ją z grafu
Obwód(u ,v):: podaj liczbę krawędzi na obwodzie „trapezu” zawierającego krawędź \(u-v\) (zakładamy, że \(u-v\) jest krawędzią zewnętrzną)
Przykład: Liczba krawędzi na obwodzie trapezu zawierającego 3-5 wynosi 5.
Uwaga: uzasadnij poprawność swoich rozwiązań i dokonaj analiz złożoności obliczeniowej zaproponowanych algorytmów.