2. Klasówka 2024/25 (10.01.2025)#
Zadanie 1 [10 punktów]#
W tym zadaniu rozważamy domknięte przedziały liczb całkowitych. Każdy przedział jest reprezentowany przez parę liczb całkowitych a, b, gdzie \(a \le b\) i a jest początkiem przedziału, natomiast b jego końcem. Skończony zbiór przedziałów S nazywamy pełnym wtedy i tylko wtedy, gdy żadne dwa przedziały z S nie mają wspólnego końca i każde dwa przedziały w tym zbiorze mają niepuste przecięcie.
[2 punkty] Dany jest pełny zbiór S złożony z n przedziałów. Zaproponuj wydajny algorytm, który znajdzie przedział będący iloczynem teoriomnogościowym wszystkich przedziałów z S.
[4 punkty] Zaproponuj strukturę danych dla dynamicznego, skończonego i pełnego zbioru przedziałów S umożliwiającą wydajne wykonywanie następujących operacji:
\(\textrm{Ini}(S):: S := \emptyset\) (Operacja wykonywana tylko raz, na samy początku).
\(\textrm{Add}(S,[a,b])::\) jeśli \(S \cup \{[a,b]\}\) jest pełny, to \(S := S \cup \{[a,b]\}\)
\(\textrm{Remove}(S,[a,b]):: S := S \setminus \{[a,b]\}\)
\(\textrm{Product}(S):: return \cap_{s \in S} s\)
[4 punkty] Rozszerz zbiór operacji z b) o dwie następujące operacje:
In(S,[a,b]):: sprawdź, czy w zbiorze S jest przedział całkowicie zawarty w [a,b]; jeśli tak, to podaj jeden z takich przedziałów
Remove2(S,[a,b]):: jeśli b jest niemniejsze od największego z początków przedziałów z S, to usuń ze zbioru S wszystkie przedziały, które mają niepuste przecięcie z przedziałem [a,b]
Zadanie 2 [6 punktów]#
[2 punkty] Dane jest drzewo binarne T z kluczami całkowitoliczbowymi w węzłach. Zaprojektuj wydajny algorytm, który sprawdzi, czy T jest drzewem wyszukiwań binarnych.
[4 punkty] Celem tego zadania jest zaprojektowanie struktury danych, która umożliwi wydajną symulację ciągu następujących operacji na początkowo pustym drzewie wyszukiwań binarnych T z kluczami całkowitoliczbowym. Klucze utożsamiamy z węzłami, w których się znajdują w drzewie.
Search(x, T):: sprawdź, czy x jest w aktualnym drzewie T
Insert(x, T):: jeśli x nie ma w drzewie T, to dodaj x do drzewa
Leaf(x,T):: sprawdź, czy x jest liściem w T
DeleteLeaf(x,T):: jeśli x jest liściem w drzewie T, to usuń x z T
Depth(x,T):: jeśli x jest w T, to podaj głębokość x w tym drzewie
Subtree(x,T):: jeśli x jest w T, to podaj liczbę węzłów w poddrzewie T o korzeniu x
Podpowiedź
Część a)
Przykłady poprawnych drzew BST:
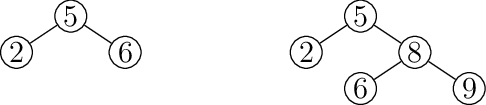
Przykłady drzew które nie są BST:

Rozwiązanie: wypisz klucze drzewa w porządku in-order i sprawdź czy otrzymany ciąg jest niemalejący.
Część b)
Struktura danych:
drzewo BST T z dodatkowymi atrybutami parent, depth, t (czas dodania węzła do drzewa), minR, maxR (minimalna i maksymalna wartość, która może zostać umieszczona w poddrzewie)
drzewo AVL A z atrybutami key, bstRef (wskaźnik od odpowiedniego węzła w T), size (rozmiar poddrzewa)
drzewo AVL L zawierające klucze odpowiadające liściom w BST
Operacje:
- Search(x, T)::
wyszukaj x w A (w czasie \(O(\log n)\)),
- Insert(x, T)::
wyszukaj pred(x, A) oraz succ(x, A) (największy klucz mniejszy niż x/najmniejszy klucz większy niż x). Niech p=pred(x).bstRef oraz s=pred(x).bstRef, klucz x będzie synem w BST węzła, który został później dodany do T (licznik t). Dodaj nowy węzeł do T, oraz zmodyfikuj drzewa A (nowy klucz), oraz drzwo L (jeden klucz przestaje być liściem oraz dodaj x). Wartościami minR/maxR są p.key+1/s.key-1 (lub \(-\infty/+\infty\)). Całość zajmuje czas \(O(\log n)\).
- Leaf(x,T)::
zwróć wartość exists(x, L),
- DeleteLeaf(x,T)::
Jeśli x nie jest liściem to nic nie rób. W przeciwnym przypadku niech v=search(x, A).bstRef, usuń v z BST, usuń x z A i L. Jeśli v.parent stał się liściem to dodaj v.parent.key do L.
- Depth(x,T)::
zwróć search(x, A).depth,
- Subtree(x,T)::
Niech p=pred(x).bstRef, zwróć wartość count(p.minR, p.maxR, A).
Zadanie 3 [4 punkty]#
Dane są trzy stosy, które początkowo zawierają po jednym żetonie każdy. Następnie wykonujemy ciąg kroków. W każdym kroku do jednego, dowolnie wybranego stosu dokładamy jeden żeton. Jeśli wysokość najwyższego stosu stanie się dwukrotnie większa od sumy wysokości dwóch pozostałych stosów, to przekładamy połowę żetonów z najwyższego stosu na pozostałe dwa stosy tak, aby na wszystkich stosach było po tyle samo żetonów. Operacjami jednostkowymi są położenie żetonu na stos i zdjęcie żetonu ze stosu.
Oblicz zamortyzowany koszt jednego kroku metodą funkcji potencjału.