2. Klasówka 2021/22 (13.01.2022)

Zadanie 1 [6 punktów]

Słowa kluczowe: amortyzacja

W tym zadaniu analizujemy grę polegającą na układaniu żetonów na nieskończonej, jednowymiarowej planszy, której pola ponumerowano kolejno \(\ldots, -2, -1, 0, 1, 2, \ldots\). Jedno posunięcie w grze polega na wybraniu pola i położeniu na nim jednego żetonu. Jeśli po położeniu żetonu okaże się, że na dwóch sąsiednich polach umieszczono tyle samo żetonów (co najmniej po jednym), to przenosimy wszystkie żetony z jednego z tych pól na drugie, czyszcząc pierwsze pole i podwajając liczbę żetonów na drugim polu. W przypadku, gdy mamy możliwość wyboru dwóch sąsiednich pól dokonujemy takiego wyboru arbitralnie. Następnie kontynuujemy opisany proces czyszczenia pola i podwajania liczby żetonów na polu sąsiednim do momentu, w którym na dwóch sąsiednich polach nie będzie tyle samo żetonów (przy czym jedno z nich musi zawierać co najmniej 1 żeton).

Przykład

Załóżmy, że na polach o numerach 1, 2, 3, 4, 5 znajduje się odpowiednio 0, 1, 2, 4 i 6 żetonów. Po dołożeniu na pole o numerze 1 jednego żetonu dostaniemy następujący układ żetonów na planszy: 0, 0, 0, 8 i 6. Elementarny ruch w grze polega na położeniu lub zdjęciu żetonu. Zatem przeniesienie k żetonów z pola na pole wymaga wykonania k operacji zdjęcia żetonu z planszy i k operacji położenia żetonu na planszy. Dokonaj analizy kosztu zamortyzowanego jednego posunięcia w grze mierzonego liczbą ruchów elementarnych.

Podpowiedź

Obserwacje:

• maksymalna wysokość stosu po n operacjach to n

• każdy element, który jest przekładany trafia na stos dwa razy większy, stąd przy n operacjach każdy żeton może zostać przełożony co najwyżej \(\log_2 n\) razy

• czyli zamortyzowany koszt pojedynczej operacji to \(O(\log n)\)

Zadanie 2 [7 punktów]

Słowa kluczowe: struktury danych, wzbogacanie

W tym zadaniu rozważamy dynamiczny, różnowartościowy ciąg liczb całkowitych C. Na ciągu C wykonujemy operacje:

• Ini(C):: C := [] // inicjacja ciągu pustego - tylko raz, na początku wykonywania wszystkich operacji

• Insert(C,x,i):: wstaw element x na pozycję i w ciągu C, \(1 \le i \le |C|+1\) //możesz przyjąć, że x nie ma w ciągu C

• Delete(C,i):: usuń i-ty element z ciągu C, \(1 \le i \le |C|`\)

• Sorted(C,i,j):: sprawdź, czy podciąg \(C_i, C_{i+1}, \ldots, C_j\) jest uporządkowany rosnąco, \(1 \le i \le j \le|C|\)

• BSComp(C,i,j):: sprawdź, czy elementy \(C_i\) oraz \(C_j\) (\(1 \le i \le j \le|C|\)) byłyby porównywane ze sobą w pierwszym przebiegu sortowania tablicy \(a[1..|C|] = [C_1, C_2, \ldots, C_{|C|}]\) algorytmem BubbleSort:

for k = 1, 2, ..., |C|-1 do
    if a[k] > a[k+1] then a[k] :=: a[k+1]; //zamiana wartości zmiennych

Zaproponuj strukturę danych umożliwiającą wydajne wykonywanie powyższych operacji.

Podpowiedź

Wzbogacamy drzewo dla dynamicznego ciągu (z operacjami Ini, Insert, Delete) o dodatkowe atrybuty:

• isSorted

• firstValue

• lastValue

• maxValue

Elementy \(a[i]\) i \(a[j]\) (\(i < j\)) są porównywane wtw, gdy: \(a[i] = \max(a[1..j-1])\)

Zadanie 3 [7 punktów]

Słowa kluczowe: AVL

Dane jest AVL-drzewo T. Zaproponuj wydajny algorytm, który obliczy dla ilu węzłów zewnętrznych w T, po wstawieniu w ich miejsce nowego elementu zostanie wykonana pojedyncza rotacja, a dla ilu podwójna. Uwaga: atrybutami węzła w drzewie są: klucz, lewy, prawy - wskaźniki do korzeni odpowiednio lewego i prawego poddrzewa, wzr - współczynnik zrównoważenia; dostęp do drzewa jest dany przez wskaźnik do jego korzenia.

Przykład

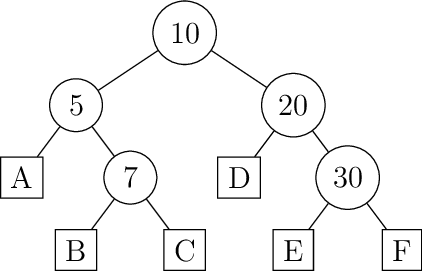
• A - 0 rotacji

• B - podwójna rotacja

• C - pojedyncza rotacja

• D - 0 rotacji

• E - podwójna rotacja

• F - pojedyncza rotacja

Wynikiem działania algorytmu będą w tym przypadku liczby 2 i 2 odpowiednio liczba węzłów zewnętrznych, dla których zostanie wykonana pojedyncza rotacja i liczba węzłów zewnętrznych, dla których zostanie wykonana podwójna rotacja.

Podpowiedź

class:

dropdown

TBD

W każdym zadaniu uzasadnij poprawność rozwiązania i dokonaj analizy złożoności obliczeniowej zaproponowanych algorytmów.