1. Klasówka 2009/10 (19.12.2009)#
Zadanie 1 [8 punktów]#
Dana jest tablica \(n \times n\), n > 1, w której w każde pole wpisano liczbę całkowitą. Chcemy przejść z dolnego lewego rogu (z (1,1)) do górnego prawego rogu (do (n,n)) i wrócić, idąc w drodze z (1,1) zawsze w prawo lub w górę, a z powrotem - w lewo lub w dół. Z danego pola można przejść tylko na pola sąsiednie (współrzędne różnią się o 1 na dokładnie jednej pozycji). Żadne pole nie może się pojawić na całej trasie (czyli tam i z powrotem) więcej niż raz, poza polem (1,1), które pojawia się na początku i na końcu trasy. Zaprojektuj algorytm znajdowania najtańszej trasy, czyli takiej, na której suma wartości pól jest najmniejsza.
Podpowiedź
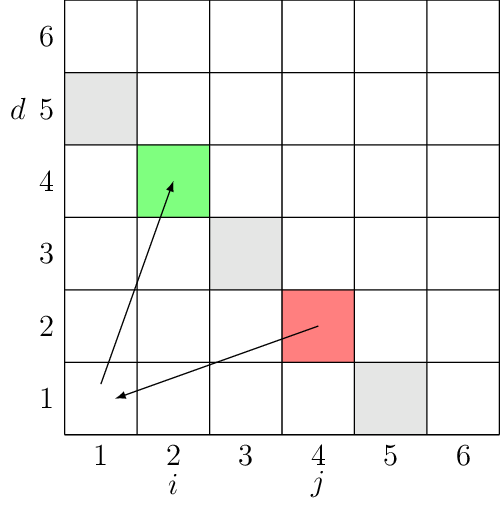
Rozwiązanie \(O(n^3)\) przez programowanie dynamiczne. \(C[d,i,j]\) (\(1\le d\le n\), \(1\le i < j\le d\)) oznacza koszt częściowego rozwiązania w którym ścieżka TAM kończy się na pozycji \((i, d+1-i)\), a ścieżka POWROTNA zaczyna się w \((j, d+1-j)\) (oba punkty na tej samej przekątnej).
Przykład: C[5,2,4]:
Zadanie 2 [7 punktów]#
Niech n będzie liczbą całkowitą większą od 1, a \(X = \{ (x,y): x = 0, 1, \ldots, n-1, y = 0, 1, 2, 3, 4 \}\) zbiorem punktów na płaszczyźnie. Danych jest n różnych prostych, z których każda przechodzi przez dwa różne punkty ze zbioru X, różniące się zawsze pierwszą współrzędną. Każda prosta zadana jest przez parę punktów \([(x_1,y_1),(x_2,y_2)]\), \(x_1 < x_2\). Zaprojektuj algorytm, który w czasie liniowym posortuje wszystkie proste niemalejąco względem ich kątów nachylenia do osi OX.
Podpowiedź
Zauważmy, że kąt nachylenia prostej \([(x_1,y_1),(x_2,y_2)]\) jest wyznaczony przez ułamek \(\alpha=\frac{y_2-y_1}{x_2-x_1}\), gdzie \((y_2-y_1) \in [-4,-3,\ldots,3,4]\). Możemy osobno posortować ułamki \(\alpha<0\), \(\alpha=0\) i \(\alpha=0\). W przypadku \(\alpha\not=0\), możemy posortować ułamki stosując sortowanie kubełkowe (wystarczy znormalizować liczniki ułamków tak by były zawsze równe 12, a wtedy liczniki są z zakresu \([0,\ldots,12n]\)).
Zadanie 3 [5 punktów]#
Podaj permutację liczb \(1, 2, \ldots, 7\), dla której algorytm HeapSort wykona największą liczbę porównań. Uwaga: należy wziąć pod uwagę obie fazy algorytmu - budowę kopca i właściwe sortowanie; poprawianie kopca odbywa się zawsze przez przesiewanie stosownego elementu w dół kopca; sortujemy rosnąco.
Uwaga: uzasadnij poprawność swoich rozwiązań oraz przeprowadź analizę złożoności obliczeniowej zaproponowanych algorytmów; każde zadanie rozwiązujemy na oddzielnej kartce.