Ctrl+K

2. Klasówka 2023/24 (11.01.2024)

2. Klasówka 2023/24 (11.01.2024)#

Zadanie 1 [7 punktów]#

Blokiem w ciągu binarnym nazywamy każdy maksymalny, spójny podciąg złożony z tych samych cyfr - zer (0) lub jedynek (1). Kompresją binarnego zapisu nieujemnej liczby całkowitej n nazywamy skończony ciąg nieujemnych liczb całkowitych K(n) zdefiniowany następująco:

  • jeśli n = 0, to K(n) = <0>;

  • dla n > 0, \(K(n) = <e_1, e_2, \ldots, e_k(n)>\), gdzie \(e_1\) jest długością bloku zbudowanego z najmniej znaczących

zer, \(e_2\) jest długością następnego bloku zbudowanego z jedynek, \(e_3\) jest długością następnego bloku zbudowanego z zer itd. na przemian długości bloków jedynek i zer. Ostatni element ciągu \(e_k(n)\) jest długością bloku zbudowanego z najbardziej znaczących jedynek. Gdy najmniej znaczącą cyfrą jest jedynka, to \(e_1\) jest zawsze równe 0.

Przykład

K(0) = <0>, K(1) = <0, 1>, K(2) = <1, 1>, K(3) = <0, 2>, K(13) = <0, 1, 1, 2>.

Zaprojektuj strukturę danych, która umożliwia efektywne wykonywanie następujących operacji na kompresji K(n) dynamicznie zmieniającej się liczby n:

  • Ini:: \(n := 0\); {operacja jest wykonywana tylko raz na samym początku}

  • Dodaj(j):: \(n := n + 2^j\) gdzie j jest nieujemną liczbą całkowitą;

  • Odejmij(j):: \(n := n - 2^j\), gdzie j jest nieujemną liczbą całkowitą taką, że \(2^j \le n\);

  • Mod(j):: \(n := n \mod 2^j\), gdzie j jest nieujemną liczbą całkowitą;

  • MaxBlok():: podaj długość najdłuższego bloku w K(n).

Zadanie 2 [6 punktów]#

Grafem trójkątów nazywamy graf spójny, w którym każda dwuspójna składowa jest cyklem o długości 3.

  1. [2 punkty] Rozważmy następujący graf trójkątów:

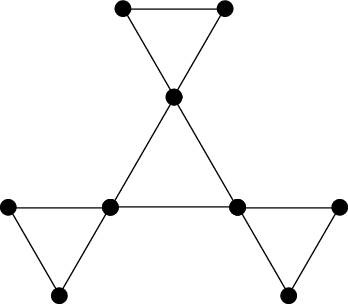
    Figure made with TikZ

    Zaznacz w tym grafie DFS-drzewa odpowiednio o najmniejszej i największej wysokości.

  2. [4 punkty] Zaprojektuj efektywny algorytm, który dla danego grafu trójkątów oblicza wysokość możliwie najwyższego DFS-drzewa.

Zadanie 3 [7 punktów]#

Powiemy, że AVL-drzewo T jest wysoce niezrównoważone, jeśli dla każdego wierzchołka w drzewie T różnego od liścia (bez następników), wysokości jego poddrzew zawsze się różnią.

  1. [2 punkty] Podaj wszystkie wartości \(n \le 100\), dla których istnieją wysoce niezrównoważone AVL-drzewa zawierające n wierzchołków.

Liczbę n, dla której istnieje n-wierzchołkowe wysoce niezrównoważone AVL-drzewo nazywamy liczbą wyjątkową. Niech n będzie liczbą wyjątkową i niech \(\langle k_1, k_2, \ldots, k_n \rangle\) będzie permutacją liczb 1, 2, ldots, n. Do początkowo pustego AVL-drzewa wstawiamy kolejno klucze \(k_1, k_2, \ldots, k_n\).

  1. [4 punkty] Zaproponuj efektywny algorytm, który wyznaczy permutację \(<k_1, k_2, \ldots, k_n>\), dla której dostaniemy wysoce niezrównoważone AVL-drzewo.

  2. [1 punkt] Dla ilu permutacji \(<k_1, k_2, k_3, k_4>\) budując 4-wierzchołkowe AVL-drzewo nie wykonamy żadnej rotacji.

Zawartość