Egzamin poprawkowy 2011/12#
Zadanie 1#
Niech T będzie \(n\)-węzłowym drzewem binarnym, w którego węzłach zapisano \(n\) parami różnych kluczy całkowitoliczbowych. Na drzewie dopuszczalne są operacje dwóch rodzajów: pojedyncza rotacja i zamiana synów węzła wraz z poddrzewami (jeden z synów może być pusty).
- Pokaż najkrótszy ciąg przekształceń, który przeprowadza drzewo
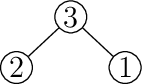
na drzewo BST.
Udowodnij, że każde drzewo binarne \(T\) z kluczami w węzłach można przekształcić na drzewo BST wykonując ciąg operacji zdefiniowanych powyżej.
Zadanie 2#
Mamy \(n\) kul ponumerowanych od \(1\) do \(n\). Na początku wszystkie kule są zielone. Na kulach wykonujemy następujące operacje:
\(Pokoloruj(a, b, kol):: 1 \leq a \leq b \leq n, kol \in \{zielony, czerwony \}\) - pokoloruj kule o numerach od \(a\) do \(b\) na kolor \(kol\),
\(Kolor(a):: 1 \leq a \leq n\) - podaj kolor kuli o numerze \(a\).
Zaproponuj strukturę danych, która umożliwi efektywne wykonanie w trybie ,,on-line” \(m\) operacji Pokoloruj i Kolor.
Załóżmy, że na początku wykonujemy \(m \geq n\) z góry znanych operacji Pokoloruj, a następnie pytamy o kolor każdej kuli. Zaproponuj efektywny algorytm obliczający kolory wszystkich kul po wykonaniu wszystkich operacji Pokoloruj.
Zadanie 3#
Podaj przykłady słów nad alfabetem \(\{a, b\}\), dla których tablice prefikso-sufiksów są postaci: \([0, 0, 1, 2, 3, 4, 5]\), \([0, 0, 1, 0, 1, 0, 1, 0, 1]\), \([0, 0, 1, 2, 3, 0, 1, 2, 3]\). (Uwaga: tablice są indeksowane od \(0\); pierwszy znak słowa jest na pozycji 1.)
Zaprojektuj efektywny algorytm, który dla danego słowa \(u\) oblicza najkrótsze słowo \(w\) takie, że \(u\) jest podsłowem (spójnym fragmentem) słowa \(ww\).