1. Klasówka 2023/24 (23.11.2023)#
Zadanie 1 [4 punkty]#
Danych jest ciąg sześciu różnych liczb całkowitych \(a_1, a_2, a_3, b_1, b_2, b_3\), o których wiadomo, że po posortowaniu żadne dwie liczby z ciągu a nie sąsiadują ze sobą.
Przykład
Powyższy warunek spełnia np. ciąg liczb 5, 1, 9, 6, 4, 2, natomiast nie spełnia go ciąg 4, 6, 1, 7, 2, 8.
Zaproponuj optymalny algorytm ze względu na liczbę porównań sortujący ciągi powyższej postaci. Udowodnij optymalność swojego rozwiązania.
Podpowiedź
Zauważy, że istnieje \(3!\cdot 3!\cdot 4\) różnych możliwych wynikóW (3! możliwości na uporządkowanie elementów \(a_1,a_2,a_3\) oraz \(a_1,a_2,a_3\) oraz 4 możliwe typy wyniku: \(ababab\) lub \(bababa\) lub \(abbaba\) lub \(ababba\)). Czyli konieczne jest co najmniej \(\lceil \log_2 144\rceil=8\) porównań.
Przykładowy algorytm:
posortuj elementy \(a_1,a_2,a_3\) (3 porównania)
posortuj elementy \(b_1,b_2,b_3\) (3 porównania)
bez straty ogólności możemy założyć, że \(a_1 < a_2 < a_3\) i \(b_1 < b_2 < b_3\)
jeśli \(a_2 < b_2\) to wynik jest typu \(ababab\) lub \(ababba\) te dwa przypadki rozróżnimy porównując \(a_3\) i \(b_3\)
wpp wynik jest typu \(bababa\) lub \(abbaba\), te dwa przypadki rozróżnimy porównując \(a_1\) i \(b_1\)
Zadanie 2 [6 punktów]#
Dana jest szachownica \(n \times n\), której wiersze i kolumny ponumerowano odpowiednio z dołu do góry i z lewa na prawo kolejno \(1, 2, \ldots, n\). O polu na przecięciu wiersza w i kolumny k mówimy, że jest polem (w,k). Na polach szachownicy ustawiono n białych gońców i n czarnych gońców, po co najwyżej 1 gońcu na jednym polu. Powiemy, że dwa gońce atakują się wtedy i tylko wtedy, gdy są różnego koloru i znajdują się na tej samej przekątnej na szachownicy i między nimi na tej przekątnej nie ma żadnego innego gońca. Dany jest ciąg składający się z 2n pól szachownicy, na których ustawiono gońców. Pierwszych n pól, to pozycje białych gońców, a ostanie n pól to pozycje czarnych gońców. Zaprojektuj efektywny algorytm, który obliczy liczbę par wzajemnie atakujących się gońców. Przykład Dla poniższego układu gońców, liczba par atakujących się gońców wynosi 4.
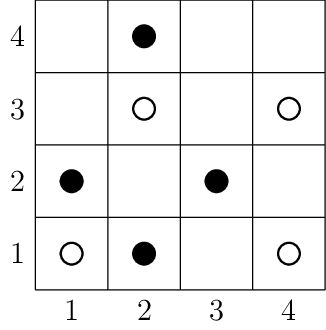
Zadanie 3 [4 punkty]#
Niech A, B będą skończonymi, niepustymi multizbiorami. Wszystkie elementy ze zbioru A są pokolorowane tym samym kolorem, powiedzmy a. Podobnie wszystkie elementy ze zbioru B są pokolorowane tym samym kolorem b. Kolory a i b są różne. Rozważmy procedurę Join(A,B), która łączy zbiory A i B w jeden zbiór i przekolorowuje elementy z mniej liczniejszego zbioru na kolor elementów z liczniejszego zbioru.
func Join(A,B) {
if |A| <= |B| then
zmień kolor każdego elementu z A na kolor elementów z B
else
zmień kolor każdego elementu z B na kolor elementów z A;
return A + B # suma zbiorów
}
Przyjmujemy, że koszt wykonania Join wynosi \(\min\{|A|, |B|\}\). Załóżmy, że mamy zbiór S złożony z n jednoelementowych zbiorów {1}, {2}, …, {n}. Przyjmujemy, że kolorem elementu i jest i. Dokonaj analizy kosztu wykonania poniższego algorytmu jako sumy kosztów operacji Join.
while |S| > 1 do {
weź dowolne dwa zbiory A i B z S;
S := S \ {A,B};
S := S + Join(A,B) # suma zbiorów
}
Zadanie 4 [6 punktów]#
W każde pole prostokątnej planszy \(2 \times n\) jest wpisana liczba całkowita. Rozmieszczenie kamieni domina \(1 \times 2\) na tej planszy polega na położeniu na niej pewnej liczby kamieni w taki sposób, żeby każdy kamień zajmował dwa pola i żadne pole nie było przykryte przez więcej niż jeden kamień. Wartością takiego rozmieszczenia jest suma liczb na przykrytych polach. Przyjmujemy, że puste rozmieszczenie (nie położono żadnego kamienia) ma wartość 0. Zaproponuj efektywny algorytm obliczania rozmieszczenia o największej wartości. Przykład Rozważmy planszę \(2 \times 7\) i rozmieszczenie czterech kostek 1 x 2.
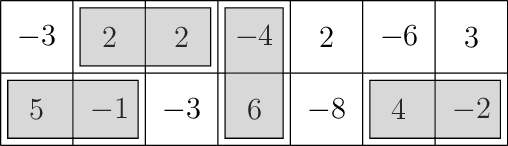
Wartością tego rozmieszczenia jest (5 + (-1)) + (2 + 2) + (-4 + 6) + (4 + (-2)) = 12. To rozmieszczenie nie jest optymalne.
Uwaga: uzasadnij poprawność swoich rozwiązań i dokonaj analizy złożoności obliczeniowej zaproponowanych algorytmów