Egzamin poprawkowy 2013/14#
Zadanie 1#
Rozważmy rekurencyjny algorytm QuickSort sortujący różnowartościowe ciągi liczbowe w taki sposób, że elementem dzielącym jest zawsze pierwszy element sortowanego ciągu, a względny porządek elementów w sortowanych rekurencyjnie podciągach jest taki sam, jak w całym ciągu. Dla ustalonego ciągu, sortowanie można przedstawić w postaci drzewa binarnego, w którego węzłach są zapisywane elementy dzielące, a dla każdego węzła lewe poddrzewo zawiera elementy mniejsze od elementu dzielącego, natomiast prawe poddrzewo - elementy większe. Takie drzewo nazywamy drzewem \(QS\).
Oto drzewo QS dla ciągu 3,4,2,1,6,7,5 (wysokość tego drzewa wynosi 3):
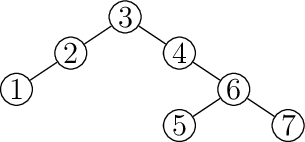
Ile jest permutacji liczb \(1, 2, 3, 4, 5\), dla których drzewo \(QS\) ma wysokość \(3\)?
Dane jest \(n\)-węzłowe drzewo binarne \(T\). Zaproponuj efektywny algorytm, który obliczy liczbę permutacji liczb \(1, 2, \cdots, n\), dla których drzewa \(QS\) i drzewo \(T\) są izomorficzne jako drzewa binarne. Możesz przyjąć, że operacje arytmetyczne są wykonywane w stałym czasie, niezależnie od wielkości argumentów.
Zaprojektuj efektywny algorytm, który dla danych: dodatniej liczby całkowitej \(n\), różnowartościowego ciągu liczb całkowitych długości \(n\) oraz liczby naturalnej \(k\), \(1 \le k \le n\), wyznaczy liczbę porównań w algorytmie \(QS\), w których bierze udział \(k\)-ty element ciągu. W przykładzie powyżej \(5\)-tym elementem ciągu jest \(6\) i bierze on udział w czterech porównaniach.
Zaprojektuj algorytm, który dla danej permutacji liczb \(1, 2, \cdots,n\) obliczy w czasie liniowym liczbę porównań wykonywanych przez algorytm QuickSort przy sortowaniu tej permutacji.
Zadanie 2#
Dla permutacji \(p\) liczb naturalnych \(1, 2, \cdots, n\), grafem inwersji nazywamy graf \(G_p = (\{1, 2, \cdots, n\}, E)\), w którym \(i \leftrightarrow j\) jest krawędzią wtedy i tylko wtedy, gdy para \((i, j)\) jest w inwersji w \(p\).
Zaprojektuj efektywny algorytm, który sprawdzi, czy dany graf \(G = (\{1, 2, \cdots, n\}, E)\) jest grafem inwersji dla pewnej permutacji \(p\) liczb naturalnych \(1, 2, \cdots, n\).
Zaprojektuj efektywny algorytm, który dla danej permutacji \(p\) obliczy liczbę spójnych składowych w grafie \(G_p\).