1. Klasówka 2025/26 (24.11.2025)#
Zadanie 1 [13 punktów]#
Niech \(n = 2^{h+1} - 1\), dla \(h \ge 3\). W tym zadaniu rozważamy pełne drzewo binarne o wysokości h, w którego węzłach zapisano liczby całkowite. Węzły drzewa są ponumerowane kolejnymi liczbami całkowitymi \(1, 2, \ldots, n\), poczynając od korzenia i kolejno poziomami, na każdym poziomie z lewa na prawo. Drzewo jest ukryte w tablicy \(a[1,\ldots,n]\) w taki sposób, że a[i] jest liczbą zapisaną w węźle o numerze i. Od tego momentu tablicę a będziemy utożsamiali z ukrytym w niej drzewem. Wagą drzewa (poddrzewa) nazywamy sumę liczb zapisanych w jego węzłach
[4 punkty] Zaprojektuj efektywny algorytm, który wyznaczy wagę najlżejszego poddrzewa drzewa a, złożonego z jego korzenia i wszystkich węzłów na ścieżkach z korzenia do trzech różnych węzłów z poziomu h (liści).
[3 punkty] Dana jest liczba całkowita k, \(1 \le k \le 2^h\). Zaprojektuj efektywny algorytm, który wyznaczy wagę najlżejszego poddrzewa drzewa a o korzeniu w węźle 1, powstającego przez usunięcie z a dokładnie k węzłów z poziomu h (liści).
[6 punktów] Załóżmy, że w każdym węźle drzewa a zapisano 0 lub 1, przy czym zapisano co najmniej jedną liczbę 1. Poddrzewem jedynkowym drzewa a nazywamy każde jego maksymalne poddrzewo binarne (nie można dodać już żadnego innego węzła), w którego węzłach zapisano same jedynki (liczby 1). Korzeniem takiego drzewa jest węzeł położony najwyżej w drzewie. Zaprojektuj efektywny algorytm, który policzy liczbę klas abstrakcji w relacji izomorfizmu dla poddrzew jedynkowych danego drzewa z zerami i jedynkami w węzłach. Zwróć uwagę, że krawędzie do lewego i prawego dziecka są rozróżnialne.
Przykład do zadania 1:
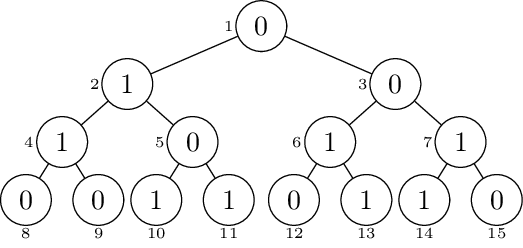
Odp. 3 b) Odp. dla k = 4 wynosi 4 c) Odp. 3
Podpowiedź
Bardziej skomplikowany przykład do podpunktu a)
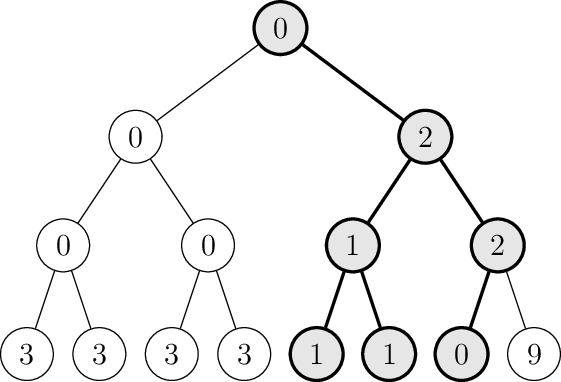
Odpowiedzią dla takiego drzewa jest 7
Zadanie 2 [3 punkty]#
Zaproponuj optymalny ze względu na porównania algorytm sortujący 7 liczb \(x_1, x_2, x_3, x_4, x_5, x_6, x_7\), o których wiadomo, że \(x_2 < x_1 < x_3\), \(x_4 < x_2 < x_5\) oraz \(x_6 < x_3 < x_7\).
Zadanie 3 [4 punkty]#
Na płaszczyźnie kartezjańskiej narysowano n odcinków poziomych i n odcinków pionowych. Wszystkie odcinki mieszczą się w kwadracie o rogach o współrzędnych \((-3n, 0), (0, 3n), (3n, 0), (0, -3n)\), końce mają współrzędne całkowitoliczbowe i mieszczą się na bokach kwadratu. Żadne dwa odcinki nie mają wspólnego końca. Zaprojektuj efektywny algorytm, który obliczy liczbę wszystkich przecięć odcinków pionowych i poziomych.
Uzasadnij poprawność swoich rozwiązań i dokonaj analizy złożoności obliczeniowej zaproponowanych algorytmów.